Rupture Process of the 2011 off the Pacific Coast of Tohoku Earthquake

(Mw 9.0) as Imaged with Back-Projection of Teleseismic P-waves

Dun Wang and Jim Mori

(Earth, Planets and Space, 63, 603-607, doi:10.5047/eps.2011.05.029, 2011)

---

Data

P waveforms from 414 USArray stations were used in a back projection analyses of the rupture for the March 11, 2011 Tohoku, Japan earthquake. The stations in the US are at distances of about 7100 to 10200 km (64 to 92 degrees) from the earthquake.

Fig. 1. USArray data (top) for the recorded P-wave. The waveforms have been aligned on the first arrival. Station information from http://www.usarray.org/status

Method

The back-projection method determines tests a grid of points to determine which is the best location for the source of seismic radiation in each designated time window of the P wave.The initial arrival of the first time window was assumed to come from the grid point corresponding to the earthquake hypocenter. For each subsequent time window (itim), the data were stacked assuming a source at each grid point (igrid) using the equation,

.

where s(igrid, itim) is the stack amplitude and t(ista, ipt) are time series for each station, ista., that has time points, ipt.. Relative time shifts for each time series were calculated using the theoretical travel times from the station to the grid point, using the IASPEI91 model. The grid of the 976 tested source locations for each time window is shown below.

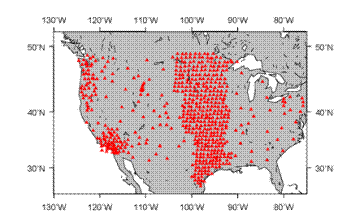
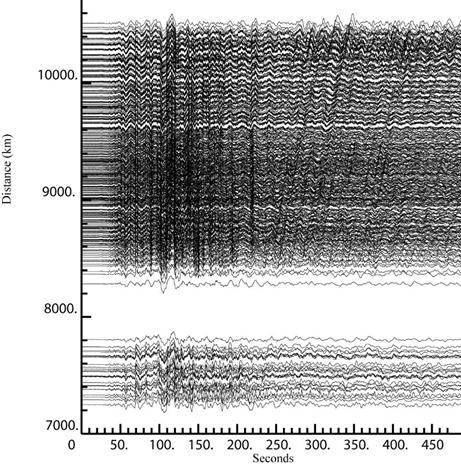
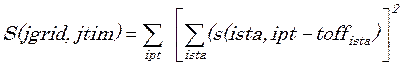
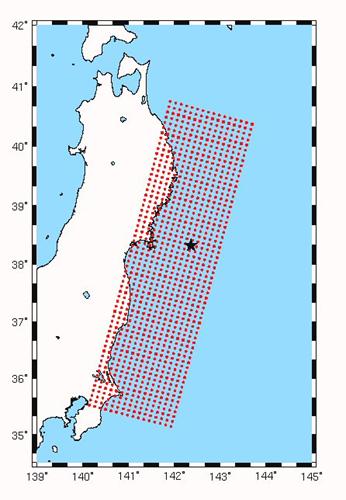
Figure 2. Grid of source locations tested for each time window.

Results

We did the back projection for both the unfiltered velocity records and filtered at 1.0 hz. The filtered version probably shows the rupture propagation better and is shown below.. The rupture progresses moves slightly toward the northwest and downdip for the first 70 sec　at a fairly slow speed of 1.0 to 1.5 km.sec. Following that, the rupture moves more rapidly toward the south.

Figure 3. Animation of the rupture propagation.

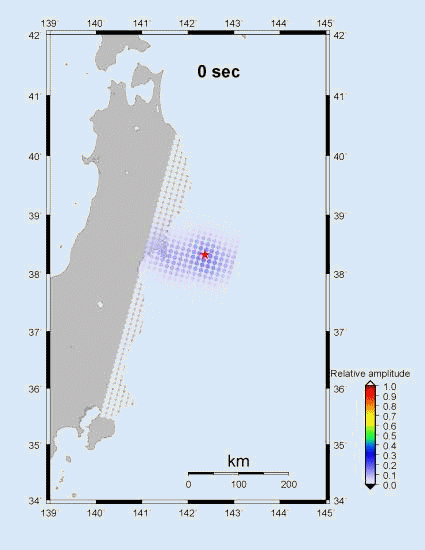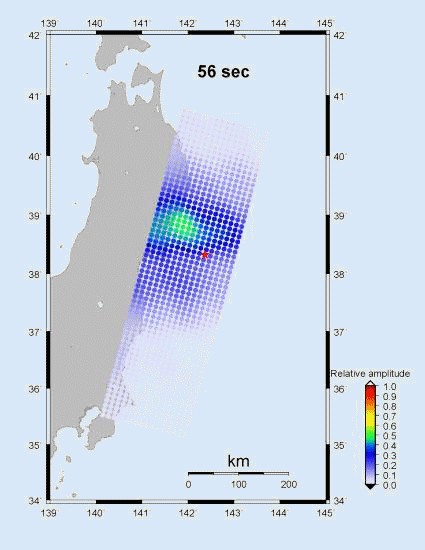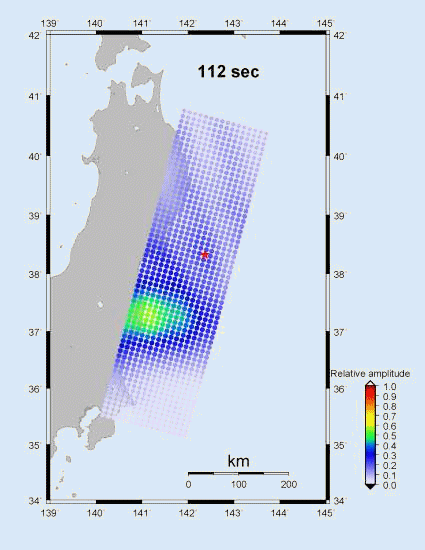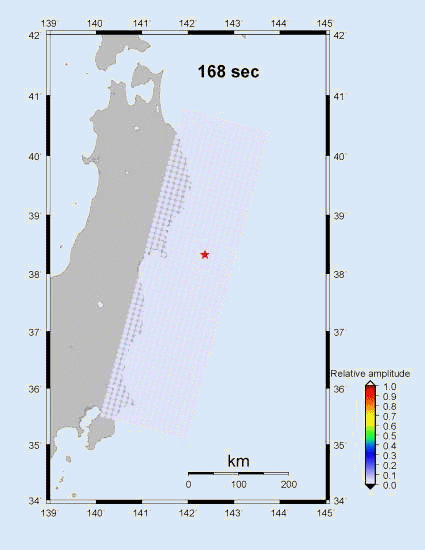
The left portion of Figure 4 shows the spatial progression of the rupture, as inferred from the location of the maximum correlation. The dots are the position for each 2 sec time point. The right portion of Figure 4 shows the position distance as a function of time.. In the top portion for the first part of the rupture, the reference position corresponding to 0 time is the epicenter. In the bottom part of the figure, the reference position is the northern most point of the second part of the rupture.

One can see that the rupture moves toward the northwest and downdip at a relative slow at a speed of about 1.0 to 1.5 km for the first 70 sec. Following that, the rupture propagates to the southwest at normal speed of about 2.5 to 3 km/sec.

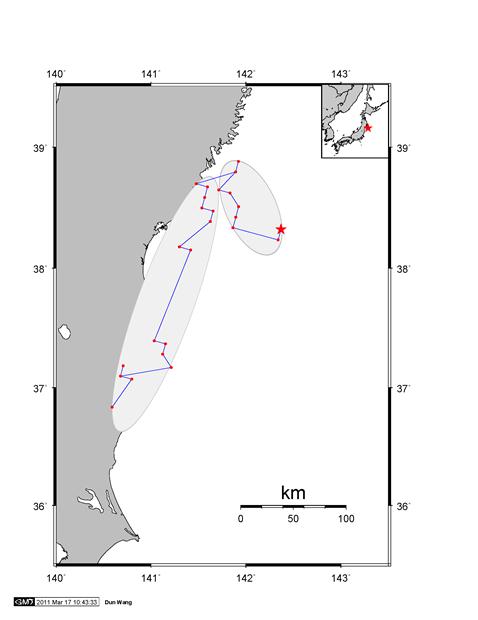
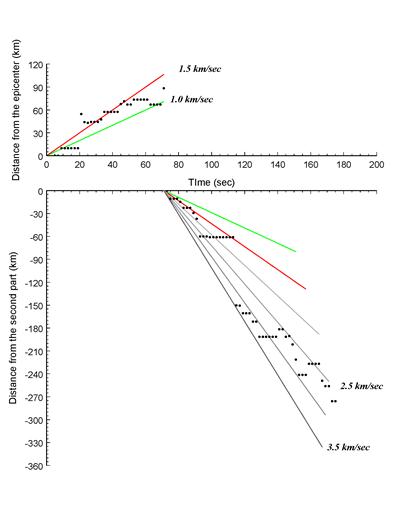
Figure 4.　Ｌｅｆｔ：　The spatial progression of the rupture from the back-projection analysis. Right: The rupture speed for the first 70 sec is 1.0 to 1.5 km/sec. The speed for the second section is 2.5 to 3.0 km/sec.

We also show the results of using different frequency bands. We carried out the back-projection analyses using data which was high-passed filtered at 1 hz (green), band-passed filtered between 0.2 and 1.0 hz (brown) and low-passed filtered at 0,2 hz (blue). Figure 5 below shows that for the lower frequency data, the locations of the inferred sources moves more toward trenchward (updip). The lowest frequency data shows sources that are trenchward of the epicenter. This is generally consistent with finite fault models which show that there is a large amount of slip on the shallow portion of the fault plane.

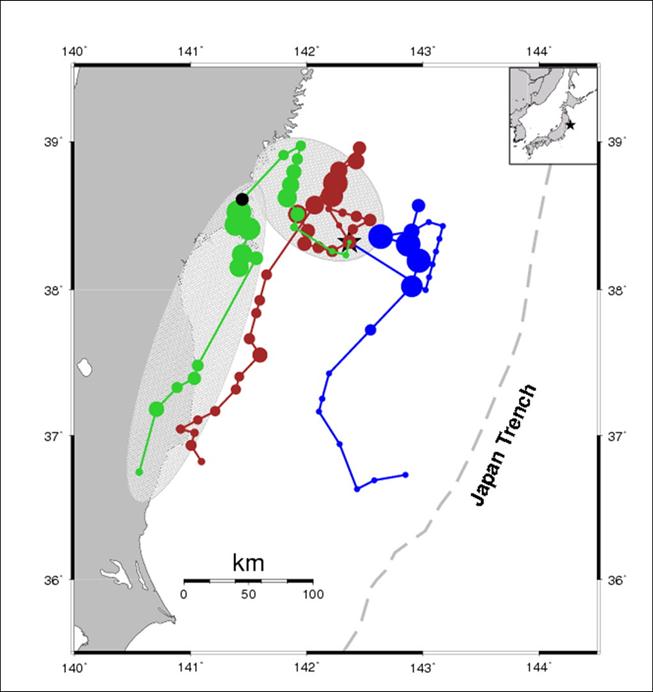
Figure 5. Sources of radiation for data high-passed filtered at 1 hz (green), band-passed filtered between 0.2 and 1.0 hz (brown) and low-passed filtered at 0.2 hz (blue).

Mori top page